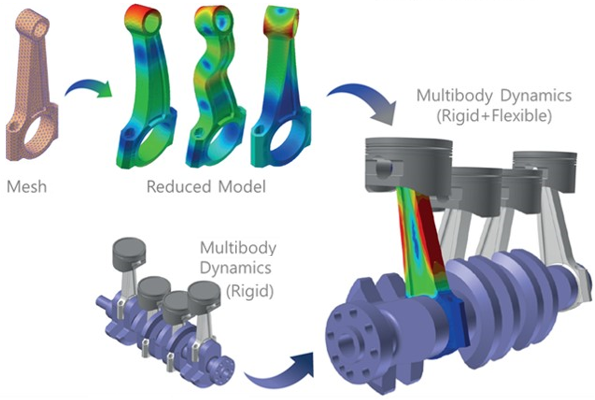
Flexible Body Analysis Using Vibration Modes
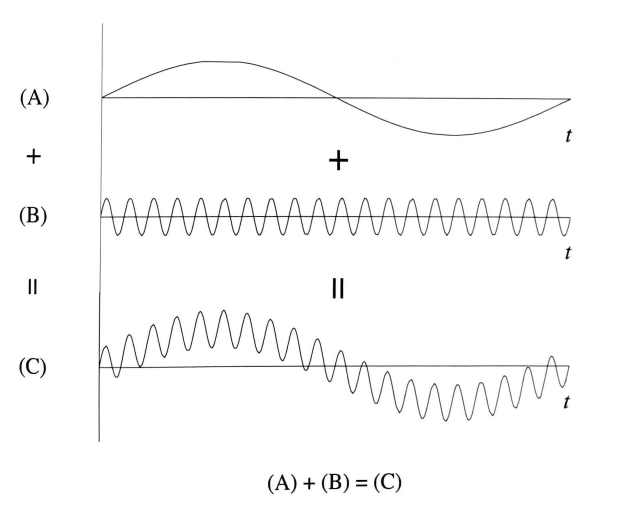
The finite element method, mentioned above, can be used to calculate the modal frequencies and mode shapes of a flexible body. The principle of superposition is used to combine individual mode shapes with weighting factors in order to reproduce any deformed shape of a flexible body. The weighting factors are also known as modal participation factors. This approach to representing flexible bodies has been offered in many dynamic simulation software for over 35 years.
Component mode synthesis (CMS) is a substructuring method that uses mode shapes and frequencies to represent the structure. CMS was originally developed to solve complex structures in a reasonable time, when computers were much slower. With multibody dynamics we are solving the flexible body several times in each time step, so even though computers are much faster today we need fast techniques to do the millions of flexible body solves that may occur during a simulation.
The use of the CMS flexible body in a multibody dynamics simulation requires the identification of attachment nodes in the finite element mesh. Some attachment nodes are located at joints/constraints and other attachment nodes are located where applied loads occur. Using finite elements software (including RFlexGen in RecurDyn) there are two sets of load cases that are investigated. First the attachment nodes at constraints are assumed to be fixed and a constrained normal modes analysis is run. Second, unit loads for each of the six degrees of freedom at each of the force attachment nodes are applied to create a set of constraint modes, which are also referred to as Craig-Bampton modes.
Advantages of Using Vibrational Modes for Flexible Body Analysis
Reduced computational complexity
CMS was developed for the reduction of finite element models and reduced computational time. For example, a detailed model, simplified model, and reduced model can all be created for the same flexible body in accordance with the degree of desired computational complexity. The starting finite element analysis model for CMS does not need to be as detailed as a model that is calculating the effect of geometric detail, such as stress concentrations. Second, the CMS model contains a small number of modes as compared to the number of finite element equations in the simplified models. In terms of computational complexity, a model with 100,000 nodes may have 300,000 equations to solve while the corresponding CMS model only has 100 equations to solve as related to the calculation of the modal participation factors as described above. Consequently, the use of flexible bodies using modes greatly reduces computational complexity, resulting in shorter computation times when arriving at solutions.
Reduction in effort needed to create flexible bodies
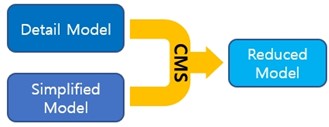 The meshes used in simplified models allow for sufficiently accurate results even if they are not as fine (small elements) as the meshes used for strength analyses (detailed model). If the subject is high frequency noise or acoustics, then a detailed model may be needed, but in general, the frequencies at issue for machinery are often in the 0 ~ 100Hz range. In such cases, creating and using a mesh that properly expresses rigidity and mass alone is not a problem. In particular, bending and torsion is extremely accurate for the low frequencies that are most often used in common machinery, so flexible bodies created by the reduction of simplified models through CMS can be used to solve machinery vibration issues.
The meshes used in simplified models allow for sufficiently accurate results even if they are not as fine (small elements) as the meshes used for strength analyses (detailed model). If the subject is high frequency noise or acoustics, then a detailed model may be needed, but in general, the frequencies at issue for machinery are often in the 0 ~ 100Hz range. In such cases, creating and using a mesh that properly expresses rigidity and mass alone is not a problem. In particular, bending and torsion is extremely accurate for the low frequencies that are most often used in common machinery, so flexible bodies created by the reduction of simplified models through CMS can be used to solve machinery vibration issues.
Limitations of Using Vibration Modes for Flexible Body Analysis
Linear Behavior
The deformation of a flexible body can be expressed as the combination of multiple mode shapes because of the principle of superposition, which only applies to linear systems. Simulation cases that are not linear systems include large overall deformations, hyper elastic materials such as rubber, and local plastic deformations. It is necessary to use RecurDyn FFlex in such cases where the flexible body behavior is nonlinear. Since generally there are small deformations involved when designing machines, most machine designs can be done with a linear analysis.
User Knowledge Required to Select Modes for MBD Simulation
The user selects the number of modes for the finite element analysis software to produce for the flexible body. In the RecurDyn multibody dynamics software the user has to decide which of the modes should be included in the model. If too many modes are included it can slow down the model run time. If too few modes are included, then the simulation results may be in error. Therefore, the user needs to make several runs initially in order to establish how many modes should be included for sufficient accuracy with a reasonable run time. This decision process is not needed when running FFlex.
Sliding and Rolling Contact
Much caution is needed when trying to include sliding or rolling contact with a modal flexible body. A contact applies a force to the body, but with sliding or rolling contact the force can’t be associated with a node because it is changing location. If the modal flexible body is quite stiff then it is possible to define such contacts if the treatment of the contact surface is carefully done.
Application of Modal Flexible Body Analysis
Flexible body analysis using vibrational modes can be used for many applications. This level of analysis is positioned between rigid body analysis that does not consider any body flexibility and complex, nonlinear flexible body analysis. A modal flexible body can produce useful results for system vibrations in the 100~200Hz range, such as might occur in the analyses of vehicle vibrations or passenger comfort. Other applications include automobiles, frames for operated machines such as construction equipment, frames for automated factory equipment, and other parts for machinery. The image portrays the simulation of an internal combustion engine with a flexible connecting rod.






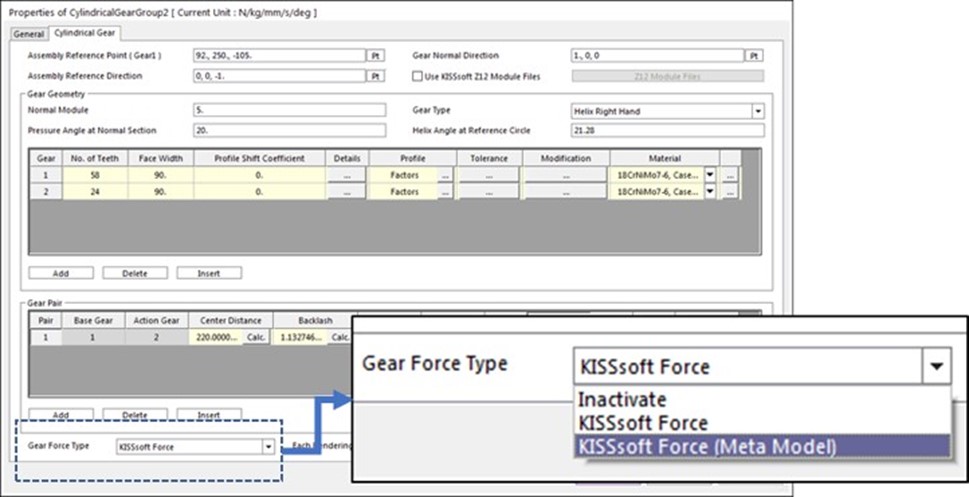
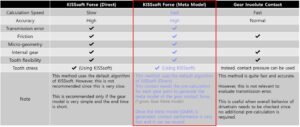
 KISSsoft Force – The gear contact is calculated by the co-simulation between RecurDyn and the embedded KISSsoft solver. Each time step, RecurDyn transfers the updated position of the gears to KISSsoft and the KISSsoft solver embedded in RecurDyn calculates the gear contact. The reaction force/torque is transferred from KISSsoft to RecurDyn.
KISSsoft Force – The gear contact is calculated by the co-simulation between RecurDyn and the embedded KISSsoft solver. Each time step, RecurDyn transfers the updated position of the gears to KISSsoft and the KISSsoft solver embedded in RecurDyn calculates the gear contact. The reaction force/torque is transferred from KISSsoft to RecurDyn.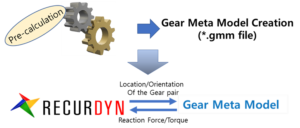
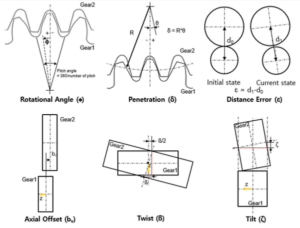




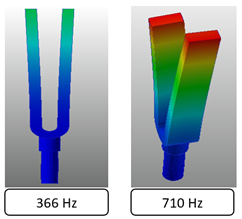
 The meshes used in simplified models allow for sufficiently accurate results even if they are not as fine (small elements) as the meshes used for strength analyses (detailed model). If the subject is high frequency noise or acoustics, then a detailed model may be needed, but in general, the frequencies at issue for machinery are often in the 0 ~ 100Hz range. In such cases, creating and using a mesh that properly expresses rigidity and mass alone is not a problem. In particular, bending and torsion is extremely accurate for the low frequencies that are most often used in common machinery, so flexible bodies created by the reduction of simplified models through CMS can be used to solve machinery vibration issues.
The meshes used in simplified models allow for sufficiently accurate results even if they are not as fine (small elements) as the meshes used for strength analyses (detailed model). If the subject is high frequency noise or acoustics, then a detailed model may be needed, but in general, the frequencies at issue for machinery are often in the 0 ~ 100Hz range. In such cases, creating and using a mesh that properly expresses rigidity and mass alone is not a problem. In particular, bending and torsion is extremely accurate for the low frequencies that are most often used in common machinery, so flexible bodies created by the reduction of simplified models through CMS can be used to solve machinery vibration issues.