Category

Modeling Methods

In Machinery General, Modeling Methods, User Tips

Using the Enhanced EHD (Elasto-Hydrodynamic Lubrication) Toolkits

Using the Enhanced EHD (Elasto-Hydrodynamic Lubrication) Toolkits

Since the release of RecurDyn V9R1 an enhanced version of the EHD (Elasto-Hydrodynamic Lubrication) toolkit has been available to RecurDyn users. Now there are actually two EHD toolkits- the Rotational Lubrication toolkit and the Piston Lubrication toolkit. These toolkits enable RecurDyn to analyze the behavior of a lubricant film in the thin gap between rapidly-moving cylindrical surfaces and the hydrodynamic forces transmitted from the lubricant to the surfaces.The Rotational Lubrication toolkit is for modeling primarily rotational motion, such as the motion found in journal bearings. The Piston Lubrication toolkit is for modeling primarily translational motion. It also supports RFlex (Flexible) Body analysis.

EHD Overview

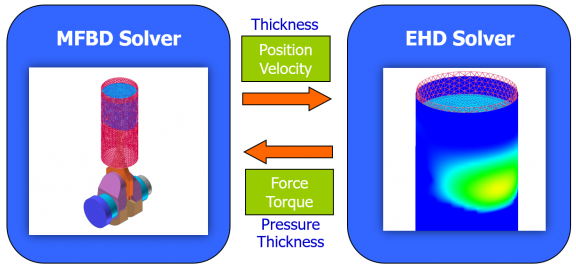
The goal of hydrodynamic lubrication is to have a lubricant that penetrates into the contact zone between rubbing solids and creates a thin liquid film. This film separates the surfaces from direct contact. In general, this reduces friction and can consequently reduce wear, since friction within the lubricant is less than between the directly contacting solids. The EHD toolkits consider viscosity and surface roughness and calculate the elastic hydrodynamic force as well as the asperity contact force. The EHD Force can be shown with a contour display and EHD results can be exported. The interactions between the mechanical model and the EHD solver is shown in the figure.

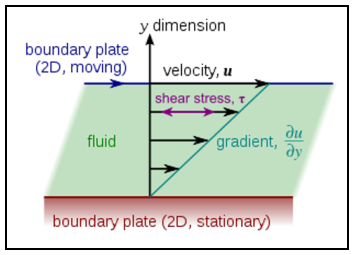
The history of lubrication theory goes back to 1886 when O. Reynolds published his famous equation of the fluid film flow in the narrow gap between two solids. The Reynolds equation carries his name and forms a foundation of the lubrication theory. The figure shows the consideration of shear stress in the fluid as a function of the relative velocity between the solid components.

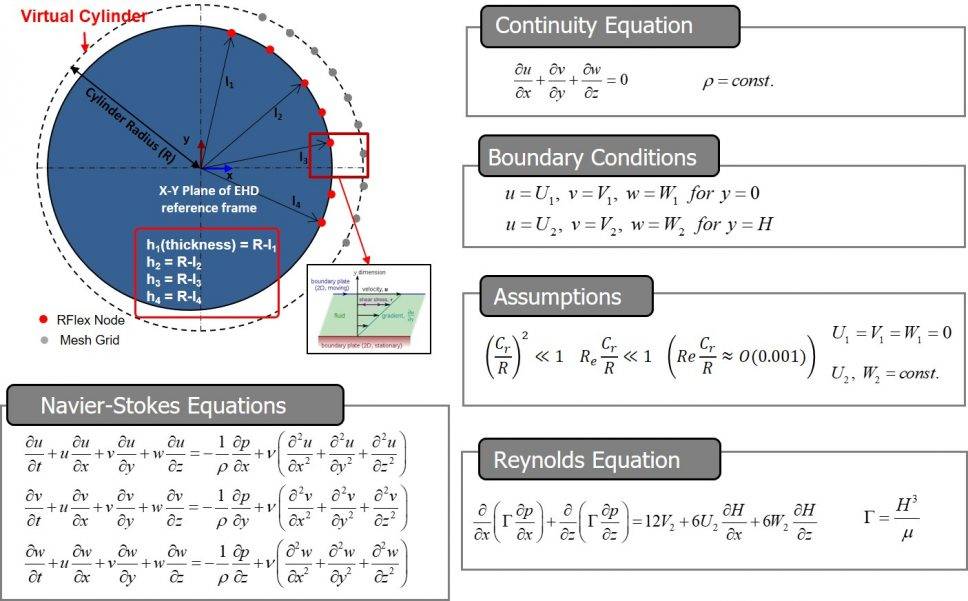
The calculation of the behavior of the local fluid lubrication region is determined by the governing equations in the figure.

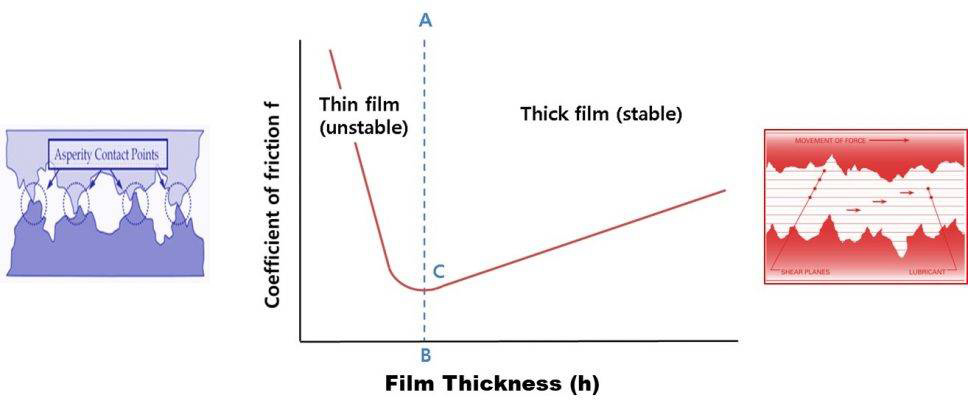
When considering the behavior of the lubrication region and the contact region there are two regimes of interest. A thin film is considered to have a height / roughness of less than 4 mm, and may have intermittent metal to metal contact. A thick film is considered to have a height / roughness of greater than 4 mm and the EHD lubrication should be stable. The figure graphically depicts these concepts.

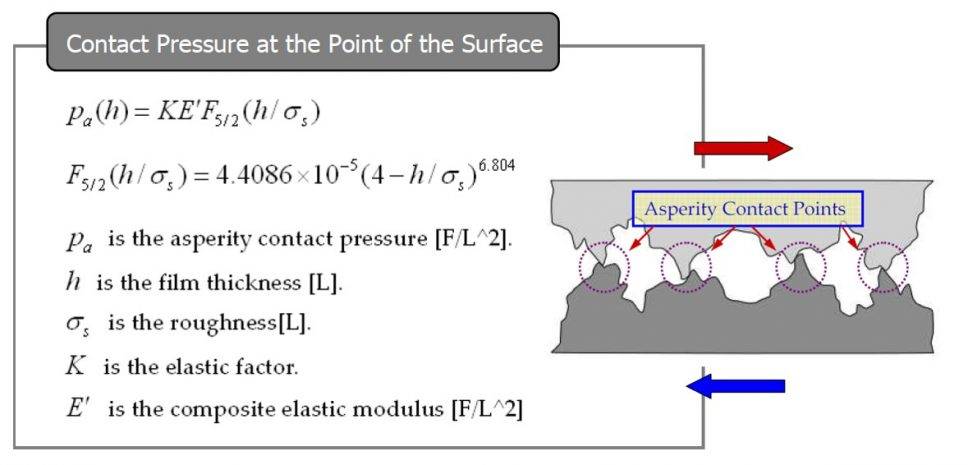
The governing equations for the contact region are given in the figure below.

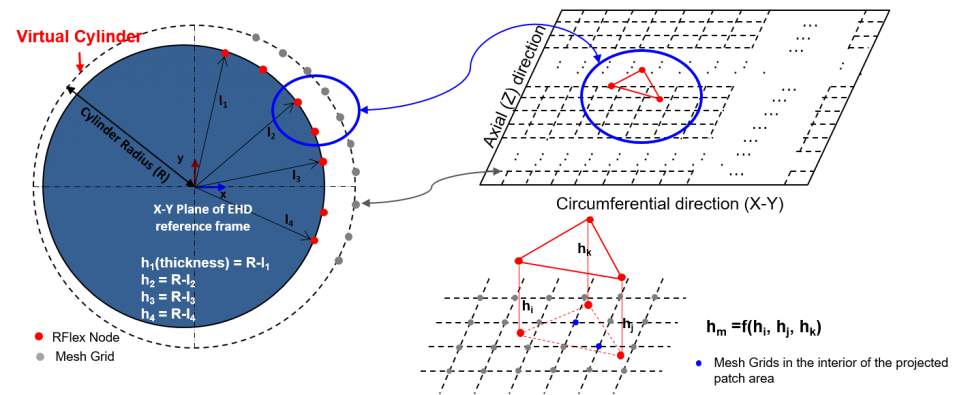
In the case of piston lubrication both the piston and the cylinder head are RFlex flexible bodies. The nodes in the piston mesh are mapped to nodes in the mesh grid of a virtual cylinder in order to detect interferences related to the contact modeling.

The EHD toolkits have their own license, so if you would like to use EHD Toolkit, please contact MotionPort to obtain a trial license. There is also a specific RecurDyn tutorial for the EHD toolkits, include pre-created example models:

In Flexible Bodies, Modeling Methods, User Tips

Tips for mesh generation – Using the Gradation Factor and Chordal Error Ratio Parameters to Control the Mesh Density

Tips for mesh generation – Using the Gradation Factor and Chordal Error Ratio Parameters to Control the Mesh Density

When you mesh complex geometry, you can improve the simulation speed and accuracy by generating a non-uniform mesh, with varying mesh density. The guiding concept is that a higher mesh density should be used in regions of high stress (and high stress gradients) while a lower mesh density can be used in area of low stress (and low stress gradients).

Note: ‘Mesh density’ is defined as the number of elements per unit distance in a mesh. A high mesh density generally produces more accurate results while a low mesh density can be simulated faster.

The RecurDyn/Mesher provides several options to generate a variable mesh efficiently. This article introduces two important parameters, the Gradation Factor and the Chordal Error Ratio. These parameters, when used properly, cause the mesh to have the proper mesh densities at curved surfaces or small features.

The definitions of the two parameters are as follows (please also refer to the images):

  • Chordal Error Ratio: It is the error between ideal curve (arc) and the approximated mesh as compared to the segment length. A smaller value produces a denser mesh on curved geometry that is more accurate.
  • Gradation Factor: It defines the rate at which the mesh transitions between high mesh density and low mesh density. The default value is 2. If you use a smaller value, the element size will vary more slowly.

A comparison of the images in the top half of the figure above shows that the reduction of the Chordal Error Ratio by a factor of 10 results in high mesh density along all of the arcs along the perimeter of the Geneva wheel as well as the circle in the center. Then, looking at the images in the bottom half of the figure shows that an 80% reduction of the Gradation Factor results in a much slower transition from a high-density mesh to a low-density mesh.

The best practice is to adjust these two parameters such that the transition in mesh density matches the transition of strain energy in the structure, while keeping the total number of nodes and elements low enough to allow for reasonable simulation times.